Station to Station Encryption in Python

Alice and Bob are looking for a more secure way to communicate than HTTPS. Sure, HTTPS is good for securing their messages against basic eavesdroppers. However, they want to secure their communication, even if someone steals their server's private key. Furthermore, Alice and Bob want to make sure that if an encryption key for any communication is broken it does not compromise the rest. The method they settle on is called the "Station To Station Protocol".

First, Alice and Bob choose a group key. This is a shared number that does not have to be private. In the math it identified as the variable g. Let me use the example 134513489037423. In reality, this number would be hundreds (or thousands) of bits long. It would satisfy a couple of important cryptographic requirements. For example, g should be the generator of a cyclic group. To start, Bob and Alice exchange Public RSA Keys. That is all the setup. Now here is an example of authentication and encryption:

Alice and Bob decide on the Group key 134513489037423
Alice chose (x) = 6334505434526010
Bob chose (y) = 8394371480300793
Alice sends Bob (g^x) 6468857056983381

Bob shared secret ((gx)^y) = 3188102960160195
Bob concatenates the exponent string (gy,gx) 64688570569833818394371480300793
Bob Sends Alice : 64688570569833818394371480300793
With the RSA Signature: eZWqjXyqrJJ9eJN4hKqmg6plimpqfoemgHVhf6SaaquLf36BhH2knp2Do2WXanGPeaCjpmORqXKkX4Z7gHJwgol-raNpqnywZpeJaDpooXybiIZonKGnn46GeWdpaKyobIN-gXd8inylqnWkfX-yaXybsZKfgoGJapt7j6Gki2pmq6CHdJ1mgqebg4KBXHCmp5hqoImRqK1-OpRnYamGZl6HaK6bpYCHqWOpeJyrnXiHaI9jYKSaqWibeY-EiJ97Zn6Cplybgp2td6RumHOAqn5zgWiJl3SyjJuafnSVm49_qZxnYH88g2-jqWd8m7KkhHWxm6WDrIWceaGpp4qphZmYhKZmiF1yf5ySoapngq2ri6iyYXhlhHeohZmcZadpmaSCaVybXXGaaaKpnGeneKKnnkKdk4CymIiZZamcnWuaZGeAh5yTgpiogpx-fZutY2SkZ6ljq6qrl25zOg==

Alice verifies the signed exponent and generates the shared secret 3188102960160195
Alice concatenates the exponent string (gx,gy) 64688570569833818394371480300793
Alice Sends Bob : 83943714803007936468857056983381
With the RSA Signature:dWiasaeEaLCip2KooGmCoXWFp56HdGVui2Slg4eSjaqqZqStf5yZoImIpqh3qohmdoWkpopiZ4-ElmBsc2eHbo2ka4FnqqyQqaJ7aDqWhaWXla57amWckn2pnJ58YalqdGqej4GKd5KMZ3eudYeIgHZneauYc2VvfpKheISbjG6Jdm6toIh-n6OTdJqfl4KLlKR6pXh2oIBnOqJ7npmtbqVgmWtqaJiyaXZ_gJycao6FoGpqe4qDk2ymgGmpiYyoeImSnpp1hHCXo56gnIloln1nmYZlYpaOeJZ4oXGXnIGpfXGGl6g8q591dH-qd3qMq4CvkoWDjHx3cotpmJOdjHx5h52WemOHbWChoIWcq5peYH2unKOWnJ2VqIh8d456hGKyaaeYmpCjoGGHpaN-ZpSngUJhZ4Z8kHearJd8hHqpfmlwY3SYbq6Wo356eayGn4B5m5RnhI2el25zOg==

Bob verifies the signed exponent string from Alice
Alice and Bob are now mutually authenticated and have a shared secret.
This secret key can then be used to encrypt further communication.

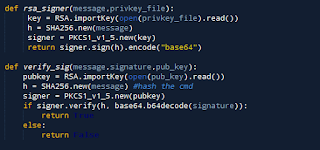
The astute reader will notice I abstracted some of that code with 4 functions. 1 for signing strings, 1 for verifying signatures, 1 to encode information wit the shared secret and one to decode it using the same key.

To use this in practical application, of course, Alice and Bob will each have a copy of the code required to compute the exponents. They will then use the network to send information back and forth to complete the handshake.